No no, no es ninguna virgen de los números ni nada de eso. en estadística la esperanza matemática, o valor esperado de una variable aleatoria, es la suma de la probabilidad de cada suceso multiplicada por su valor. Por ejemplo en un juego de azar, la esperanza es el beneficio medio:
Por mi parte, ya he hecho una porra en el curro para hacerme rico... ánimo
J.
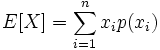





4 comentarios:
Echar todas las combinaciones son 152 millones de euros y sólo el primer premio son 180 millones. Estoy dispuesto a asumir el riesgo de que alguien más acierte. ¿Alguien me presta 152 millones de euros? :-)
No me cuadra...
Cómo que "sale mejor jugar que no hacerlo"? Vaya trola!!!!
Lo que quiere decir que la esperanza matemática sea positiva, es que por cada euro apostado, el premio medio será de más de un euro.
Se ve más fácil con el efecto contrario de la lotería por ejemplo. Qué pasa si compras todos los números? Que el premio total es menor que lo que te has gastado. (Hacienda se queda con pasta ;) ) O sea, que a nadie se le ocurre comprar todos los números.
En este caso no, el premio total es mayor que lo apostado. En tal caso, compensaría hacer todas las combinaciones posibles (siempre y cuando tú fueras el único jugador, claro!. Porque si tienes que compartir el premio, se fastidia el invento.)
Ah!, y si no juegas todas las combinaciones...empiezas a tener probabilidades de perder todo lo jugado...Y es que el premio no se distribuye uniformemente entre los participantes, sino que queda concentrado entre los pocos acertantes que haya.
Así que...que nadie se engañe. Tienes las mismas probabilidades de hacerte rico a golpe de euromillón que antes...eso sí, si te toca, igual te toca más ;)
Efectivi, no había dicho nada de que la probabilidad de que te toque la lotería sea mayor. He comentado que desde el punto de vista matemático la esperanza es positiva, es decir, desde el punto de vista matemático sale mejor jugar que no hacerlo. Creía que se entendía, pero viene siendo algo así como "si compraras todos los números, el dinero que ganarías es mayor que el que te gastas".
...en cualquier caso, muy buena la aclaración de Alfonso ;-)
Publicar un comentario